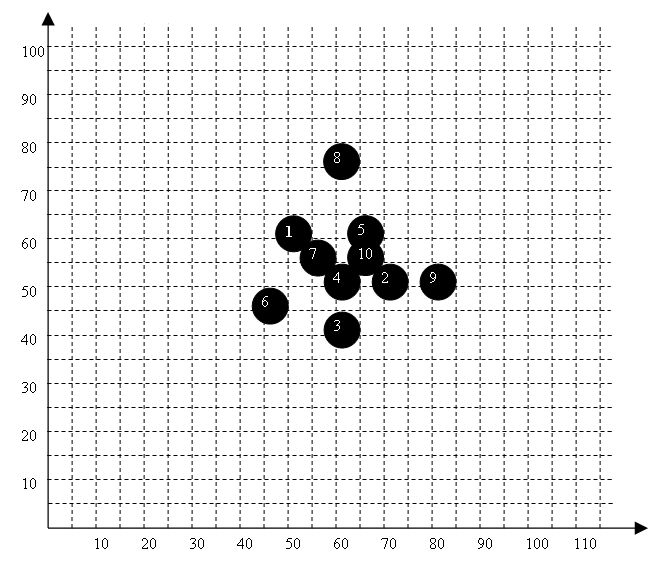
Veronderstellen we volgende groepering. Ze is geschoten met een geweer Cal .308 Winchester op 100 meter afstand.

De schoten zijn genummerd in volgorde dat ze geschoten zijn. Voor ieder schot werden de co÷rdinaten in het assenstelsel opgetekend, dit wordt weergegeven in onderstaande tabel. Merk op dat sommige doeltoestellen automatisch de co÷rdinaten van het schot geven, denk maar aan de Sius-Ascor installatie in Leopoldsburg.
| Nummer | ||
| 1 | 50 | 60 |
| 2 | 70 | 50 |
| 3 | 60 | 40 |
| 4 | 60 | 50 |
| 5 | 65 | 60 |
| 6 | 45 | 45 |
| 7 | 55 | 55 |
| 8 | 60 | 75 |
| 9 | 80 | 50 |
| 10 | 65 | 55 |
Om te beginnen kunnen we enkele basisberekeningen uitvoeren, dit kan het best gebeuren in een rekenbladtoepassing zoals Excel.
| Nr Schot | Afstand | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 50 | 60 | 61 | 54 | - 11 | 6 | 121 | 36 | 12,5300 |
| 2 | 70 | 50 | 61 | 54 | 9 | - 4 | 81 | 16 | 9,8489 |
| 3 | 60 | 40 | 61 | 54 | - 1 | - 14 | 1 | 196 | 14,0357 |
| 4 | 60 | 50 | 61 | 54 | - 1 | - 4 | 1 | 16 | 4,1231 |
| 5 | 65 | 60 | 61 | 54 | 4 | 6 | 16 | 36 | 7,2111 |
| 6 | 45 | 45 | 61 | 54 | - 16 | - 9 | 256 | 81 | 18,3576 |
| 7 | 55 | 55 | 61 | 54 | - 6 | 1 | 36 | 1 | 6,0828 |
| 8 | 60 | 75 | 61 | 54 | - 1 | 21 | 1 | 441 | 21,0238 |
| 9 | 80 | 50 | 61 | 54 | 19 | - 4 | 361 | 16 | 19,4165 |
| 10 | 65 | 55 | 61 | 54 | 4 | 1 | 16 | 1 | 4,1231 |
| Som : | 610 | 540 | 890 | 840 | 116,7524 | ||||
| Gemiddeld : | 61 | 54 | 61 | 54 | 0 | 0 | 89 | 84 | 11,6752 |
| Kleinste : | 45 | 40 | 4,1231 | ||||||
| Grootste : | 80 | 75 | 21,0238 | ||||||
| H + L : | 35 | 35 |
Op basis van deze gegevens gaan we nu specifiek de verschillende manieren om groeperingen te typeren eens toepassen.
De formules zijn de volgende :
Variantie :
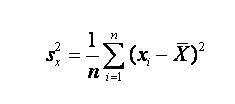
Dit is het gemiddelde van alle waarden , dit getal kunnen we direct terugvinden in onze tabel :
| Nr Schot | Afstand | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 50 | 60 | 61 | 54 | - 11 | 6 | 121 | 36 | 12,5300 |
| 2 | 70 | 50 | 61 | 54 | 9 | - 4 | 81 | 16 | 9,8489 |
| 3 | 60 | 40 | 61 | 54 | - 1 | - 14 | 1 | 196 | 14,0357 |
| 4 | 60 | 50 | 61 | 54 | - 1 | - 4 | 1 | 16 | 4,1231 |
| 5 | 65 | 60 | 61 | 54 | 4 | 6 | 16 | 36 | 7,2111 |
| 6 | 45 | 45 | 61 | 54 | - 16 | - 9 | 256 | 81 | 18,3576 |
| 7 | 55 | 55 | 61 | 54 | - 6 | 1 | 36 | 1 | 6,0828 |
| 8 | 60 | 75 | 61 | 54 | - 1 | 21 | 1 | 441 | 21,0238 |
| 9 | 80 | 50 | 61 | 54 | 19 | - 4 | 361 | 16 | 19,4165 |
| 10 | 65 | 55 | 61 | 54 | 4 | 1 | 16 | 1 | 4,1231 |
| Som : | 610 | 540 | 890 | 840 | 116,7524 | ||||
| Gemiddeld : | 61 | 54 | 61 | 54 | 0 | 0 | 89 | 84 | 11,6752 |
| Kleinste : | 45 | 40 | 4,1231 | ||||||
| Grootste : | 80 | 75 | 21,0238 | ||||||
| H + L : | 35 | 35 |
Want de variantie is niets anders dan :
De standaardafwijking is de vierkantswortel uit de variantie want :
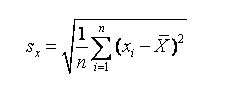
Uitgewerkt wordt dat :
Op eenzelfde manier kunnen we de waarden voor y berekenen :
De gemiddelde horizontale afwijking (GHA) kan bepaald worden als het gemiddelde van de absolute waarden van de individuele horizontale afwijkingen.
Uitgewerkt wordt dat :
Op eenzelfde manier kan de gemiddelde verticale afwijking geschreven worden (GVA):
De formule is :
Uitgewerkt wordt dat :
We sorteren de impacten van de verschillende schoten volgens hun afstand tot het GIP van klein naar groot. We vinden de getallen terug in de tabel.
| Nr Schot | Afstand | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 50 | 60 | 61 | 54 | - 11 | 6 | 121 | 36 | 12,5300 |
| 2 | 70 | 50 | 61 | 54 | 9 | - 4 | 81 | 16 | 9,8489 |
| 3 | 60 | 40 | 61 | 54 | - 1 | - 14 | 1 | 196 | 14,0357 |
| 4 | 60 | 50 | 61 | 54 | - 1 | - 4 | 1 | 16 | 4,1231 |
| 5 | 65 | 60 | 61 | 54 | 4 | 6 | 16 | 36 | 7,2111 |
| 6 | 45 | 45 | 61 | 54 | - 16 | - 9 | 256 | 81 | 18,3576 |
| 7 | 55 | 55 | 61 | 54 | - 6 | 1 | 36 | 1 | 6,0828 |
| 8 | 60 | 75 | 61 | 54 | - 1 | 21 | 1 | 441 | 21,0238 |
| 9 | 80 | 50 | 61 | 54 | 19 | - 4 | 361 | 16 | 19,4165 |
| 10 | 65 | 55 | 61 | 54 | 4 | 1 | 16 | 1 | 4,1231 |
| Som : | 610 | 540 | 890 | 840 | 116,7524 | ||||
| Gemiddeld : | 61 | 54 | 61 | 54 | 0 | 0 | 89 | 84 | 11,6752 |
| Kleinste : | 45 | 40 | 4,1231 | ||||||
| Grootste : | 80 | 75 | 21,0238 | ||||||
| H + L : | 35 | 35 |
Als we de afstanden rangschikken volgens grootte, te beginnen bij het kleinste, krijgen we volgende tabel. We zien dat het vijfde kleinste getal gelijk is aan de afstand van schot Nr 2 namelijk 9,8489. We kunnen dus zeggen dat van de tien schoten er vijf in een cirkel vallen met een straal van 9,8489. De CEP is echter de diameter, dus tweemaal de straal = 19,7.
We weten ook dat dit slechts een benadering is want bij de bepaling van de CEP gaat het over een zeer groot aantal schoten en niet over slechts tien, maar we kunnen dit aannemen als een benadering.
| Nr Schot | Afstand |
| 4 | 4,1231 |
| 10 | 4.1231 |
| 7 | 6,0828 |
| 5 | 7,2111 |
| 2 | 9,8489 |
| 1 | 12,5300 |
| 3 | 14,0357 |
| 6 | 18,3576 |
| 9 | 19,4165 |
| 8 | 21,0238 |
We kunnen zeggen dat 50% van de schoten binnen een cirkel met diameter 19,7 ligt rond het GIP.
De gemiddelde straal wordt bekomen door het gemiddelde te nemen van alle individuele afstanden van de verschillende invalspunten tot het GIP. Om die te berekenen maken we de som van alle individuele afstanden tot het GIP en delen die door het aantal schoten:
We vinden dit getal ook direct terug in de basistabel :
| Nr Schot | Afstand | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 50 | 60 | 61 | 54 | - 11 | 6 | 121 | 36 | 12,5300 |
| 2 | 70 | 50 | 61 | 54 | 9 | - 4 | 81 | 16 | 9,8489 |
| 3 | 60 | 40 | 61 | 54 | - 1 | - 14 | 1 | 196 | 14,0357 |
| 4 | 60 | 50 | 61 | 54 | - 1 | - 4 | 1 | 16 | 4,1231 |
| 5 | 65 | 60 | 61 | 54 | 4 | 6 | 16 | 36 | 7,2111 |
| 6 | 45 | 45 | 61 | 54 | - 16 | - 9 | 256 | 81 | 18,3576 |
| 7 | 55 | 55 | 61 | 54 | - 6 | 1 | 36 | 1 | 6,0828 |
| 8 | 60 | 75 | 61 | 54 | - 1 | 21 | 1 | 441 | 21,0238 |
| 9 | 80 | 50 | 61 | 54 | 19 | - 4 | 361 | 16 | 19,4165 |
| 10 | 65 | 55 | 61 | 54 | 4 | 1 | 16 | 1 | 4,1231 |
| Som : | 610 | 540 | 890 | 840 | 116,7524 | ||||
| Gemiddeld : | 61 | 54 | 61 | 54 | 0 | 0 | 89 | 84 | 11,6752 |
| Kleinste : | 45 | 40 | 4,1231 | ||||||
| Grootste : | 80 | 75 | 21,0238 | ||||||
| H + L : | 35 | 35 |
Als we kijken naar groep 1 dan zien we dat voor het berekenen van de maximale spreiding volgende koppels van schoten in aanmerking komen:
We voeren de berekeningen uit aan de hand van volgende formule :
en we krijgen volgende waarden :
| Koppel | ES |
| 3 - 8 | 35 |
| 6 - 8 | 33,54 |
| 8 - 9 | 32,02 |
We zien dat het koppel 3 - 8 het verst uit elkaar ligt, de ES van groep 1 is dus 35.
Om te controleren of de kleinste omschrijvende cirkel als middelpunt het midden heeft van de lijn tussen schot 3 en schot 8, moeten we eerst de co÷rdinaten van dat middelpunt bepalen.
We hebben geluk, beide schoten liggen juist boven elkaar, het middelpunt wordt dan :
x = 60
y = 40+35/2 = 40+17,5 = 57,5
Nu moeten we de afstand van ieder schot tot dat middelpunt bepalen en dat moet kleiner of gelijk zijn aan 17,5.
| Nr Schot | Afstand |
| 1 | 10,3078 |
| 2 | 12,500 |
| 3 | 17,5000 |
| 4 | 7,5000 |
| 5 | 5,5902 |
| 6 | 19,5256 |
| 7 | 5,5902 |
| 8 | 17,5000 |
| 9 | 21,3600 |
| 10 | 5,5902 |
We zien dat er twee schoten zijn die juist op een afstand van 17,5 liggen van dat middelpunt, dat is helemaal niet verwonderlijk want dat is hetgeen we berekend hebben door het midden van het koppel 3 - 8 te nemen als middelpunt van de omschrijvende cirkel.
Wat ons meer verontrust is het feit dat er twee getallen GROTER zijn dan 17,5. Dit wil zeggen dat die buiten een cirkel met straal 17,5 en als middelpunt het midden tussen de impacten 3 en 8, vallen. Wat we berekend hebben is dus NIET de kleinste omschrijvende cirkel. Ik heb voor het moment geen oplossing om daaraan op een eenvoudige manier te verhelpen. We kunnen hieruit alleen besluiten dat de kleinste omschrijvende cirkel een straal zal hebben die ergens tussen 17,5 en 21,36 zal liggen. (Wordt vervolgd)
Deze kunnen we direct uit de tabel met de voorbereidende berekeningen afleiden :
| Nr Schot | Afstand | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 50 | 60 | 61 | 54 | - 11 | 6 | 121 | 36 | 12,5300 |
| 2 | 70 | 50 | 61 | 54 | 9 | - 4 | 81 | 16 | 9,8489 |
| 3 | 60 | 40 | 61 | 54 | - 1 | - 14 | 1 | 196 | 14,0357 |
| 4 | 60 | 50 | 61 | 54 | - 1 | - 4 | 1 | 16 | 4,1231 |
| 5 | 65 | 60 | 61 | 54 | 4 | 6 | 16 | 36 | 7,2111 |
| 6 | 45 | 45 | 61 | 54 | - 16 | - 9 | 256 | 81 | 18,3576 |
| 7 | 55 | 55 | 61 | 54 | - 6 | 1 | 36 | 1 | 6,0828 |
| 8 | 60 | 75 | 61 | 54 | - 1 | 21 | 1 | 441 | 21,0238 |
| 9 | 80 | 50 | 61 | 54 | 19 | - 4 | 361 | 16 | 19,4165 |
| 10 | 65 | 55 | 61 | 54 | 4 | 1 | 16 | 1 | 4,1231 |
| Som : | 610 | 540 | 890 | 840 | 116,7524 | ||||
| Gemiddeld : | 61 | 54 | 61 | 54 | 0 | 0 | 89 | 84 | 11,6752 |
| Kleinste : | 45 | 40 | 4,1231 | ||||||
| Grootste : | 80 | 75 | 21,0238 | ||||||
| H + L : | 35 | 35 |
We zien dus dat : H + L = 35 + 35.
De formule is :
Bij het invullen van de waarden krijgen we :
De formule is hier :
We weten dat de groep geschoten is op 100 meter en we moeten onze ES uitdrukken in cm :
We veronderstellen dezelfde gegevens als bij de berekening van de MOA hierboven en we krijgen (opgepast: hier terug de ES uitdrukken in mm.) :
Wanneer we groeperingen meten, kunnen we dat doen op twee manieren. We kunnen de buitenste merktekens van een groep nemen.
Bijvoorbeeld :
Als we echter de gegevens gaan
gebruiken voor berekeningen moeten we de afstand d weten tussen de
centers van de schoten d(ctc).