Er bestaat een groot aantal manieren om een geschoten groepering te meten. Welke manier de beste is, heeft in het verleden al geleid tot eindeloze discussies. Volgens mij is er geen "beste" methode, maar bestaan er een reeks metingen en berekeningen die, naargelang de situatie, beter geschikt zijn en/of meer inlichtingen geven. Een grondige studie vereist een goede kennis van de statistiek en dit valt buiten het bestek van dit hoofdstuk. We gaan ons hier beperken tot een opsomming van de verschillende methodes met de uitleg over de verschillende berekeningen. Geïnteresseerden in dit onderwerp kunnen zich verdiepen in de statistiek, er is daar meer dan voldoende informatie over te verkrijgen, onder andere op het Internet.
Talrijke testen hebben uitgewezen dat de spreiding van de impact van projectielen rond een mikpunt volledig willekeurig van natuur is. Het fenomeen kan dus op een statistische manier benaderd worden gezien de proefondervindelijke spreiding een Gauss-kurve volgt.
Het feit dat er altijd een spreiding is van de invalspunten is te wijten aan:
Het is van belang te weten dat de grootte van de groep, in meer of mindere mate, altijd zal afhangen van het aantal schoten in de groep.
In dit kader moet vermeld
worden dat de meest toegepaste methode om groeperingen te meten die is
van de "grootste spreiding" (Engels: Extreme spread, ES) waarbij de
afstand tussen de twee impacten die het verst uit elkaar liggen
gebruikt wordt als maataanduiding van de groepering. Men kan zich
hierbij voorstellen dat voor een groep bestaande uit een aantal dicht
bij elkaar liggende schoten met één enkele schot
duidelijk buiten deze kern (flyer), deze laatste een invloed buiten
proportie zal hebben op de grootte van de groep. Niettegenstaande dit
laatste wordt de methode bijna universeel toegepast buiten de
gespecialiseerde wereld van ballistische labo's en wapenfabrieken. Het
quasi universeel gebruik van deze methode en de aandacht die in
verschillende schootsdisciplines aan de meting van groeperingen besteed
wordt, heeft waarschijnlijk de grootste bijdrage geleverd aan de
verbetering van de kwaliteitscontrole bij de verschillende wapen- en
munitiefabrikanten. Inderdaad de precisie en de kwaliteit van de
huidige beschikbare munitie en wapens is beter dan ooit.
(Ref: A.B. BAILEY in Guns Review, Juli, 1989).
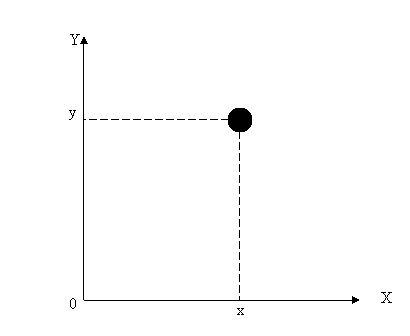
Om een statistische evaluatie van een groepering te kunnen uitvoeren moeten er gegevens verzameld worden over elk schot in de groepering. Men kan dat doen door een assenstelsel met vierkantennet over de groep te plaatsen en voor ieder schot de coördinaten (x,y) te noteren.

Voor impact 1 krijgen we de waarden (x1, y1); voor impact 2 (x2, y2); voor impact i (xi, yi) enzoverder tot de laatste impact. Voor een groep van n schoten is dat impact n (xn, yn).
De oorsprong van het assenstelsel (de kruising van de X- en de Y-as waar de 0 staat) kan in het midden van de groep geplaatst worden maar dikwijls wordt het onder links van de groep geplaatst. Op die manier zijn alle x en y gegevens die men noteert positief. Dit voorkomt rekenfouten.
Men kan nu de gemiddelde waarde (![]() )
van de horizontale coördinaten berekenen op volgende manier.
Men neemt de som van alle x-waarden, voor n schoten is dat:
)
van de horizontale coördinaten berekenen op volgende manier.
Men neemt de som van alle x-waarden, voor n schoten is dat:
![]()
en men deelt die door het aantal schoten in de groep (hier: n).De formule wordt:
![]()
Een gelijkaardige formule kan geschreven worden voor de y-waarden.
![]()
We krijgen dus twee gemiddelde waarden en dit zijn de coördinaten van het GEMIDDELD INVALSPUNT (GIP).
Het GIP is het statistische middelpunt van de groep invalspunten (de groepering).
Hier dient opgemerkt te worden dat het gemiddeld invalspunt meestal niet overeenkomt met het MIKPUNT (MP).
Het laten samenvallen (of zo dicht mogelijk bij elkaar brengen) van het GIP en het MP noemt men "justeren". Men doet dat door de mikinrichting bij te regelen.
Men kan spreken over de juistheid van het schieten als men het heeft over hoever het GIP van het MP gelegen is.
Onder precisie verstaat men de spreiding van de individuele schoten rond het GIP (hier in feite de grootte van de groepering).
Wanneer er een nieuwe groep geschoten wordt dan zal het GIP op een andere plaats liggen dan bij de eerste groep. Merk ook op dat het GIP zich bij ieder bijkomend schot verplaatst.
Het mikpunt blijft in principe hetzelfde.
De mate waarin het GIP varieert van plaats zal een functie zijn van de grootte van de groepering en van het aantal schoten.

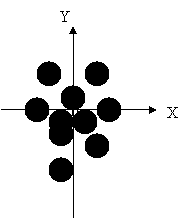
Bovenstaande groepering is geschoten met een wapen dat tamelijk precies is maar niet gejusteerd.

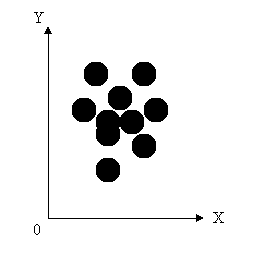
Hier ziet men een groepering van een wapen dat gejusteerd is en tamelijk precies.

Hier is het wapen goed gejusteerd maar het is helemaal niet precies.
De verplaatsing van het GIP in functie van de bijkomende schoten.

Na twee schoten ligt het GIP op deze plaats.
Een bijkomend schot zorgt voor de verplaatsing van het GIP.

In dit onderdeel zal gesproken worden over de volgende methoden om de grootte van een groepering uit te drukken:
De afwijking van ieder schot kan beschouwd worden als de afstand van
het midden van het impact tot het GIP. Men kan de afwijking van een
schot uitdrukken aan de hand van zijn coördinaten. Inderdaad
wanneer een schot i de coördinaten (xi,yi) heeft en het GIP de
coördinaten ![]() dan is de afwijking van het schot i
dan is de afwijking van het schot i
Horizontaal:![]()
Vertikaal:![]()
De afstand di van het schot i tot het GIP wordt (Stelling van Pythagoras)
![]()
Onder standaardafwijking (s) verstaat men het gemiddelde van de afwijkingen (afzonderlijk horizontaal en vertikaal) van ieder schot ten opzichte van het GIP.
Wanneer men daarover nadenkt dan komt men tot de conclusie dat bij het gewoon berekenen van de gemiddelde horizontale en verticale afwijking men altijd op "0" uitkomt. Eenvoudig gezegd is de reden omdat er evenveel schot links van het GIP liggen als er schoten rechts ervan liggen. Dezelfde redenering gaat op voor erboven en eronder.
Om dit op te lossen passen we een kleine 'truk' toe. We kwadrateren (vermenigvuldigen met zichzelf) iedere individuele afwijking, berekenen daar het gemiddelde uit en trekken dan de vierkantswortel uit het resultaat.
Dit wordt:
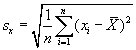
Of nog:
![]()
dit wordt ook de variantie genoemd.
Als we daar enkele berekeningen op uitvoeren dan krijgen we eerst:
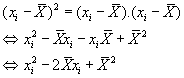
Plaatsen we dat in de formule van de variantie dan krijgen we:
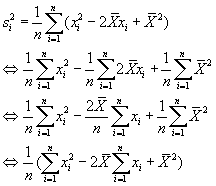
We weten ook dat :
![]()
En we krijgen dus:
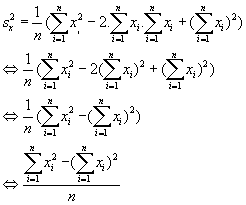
Vervolgens wordt de horizontale standaardafwijking:
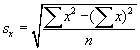
Met een volkomen analoge redenering kunnen we de verticale standaardafwijking als volgt noteren:
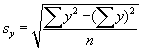
De gemiddelde horizontale afwijking (GHA) kan bepaald worden als het gemiddelde van de absolute waarden van de individuele horizontale afwijkingen.
![]()
Op eenzelfde manier kan de gemiddelde verticale afwijking geschreven worden (GVA):
![]()
In het Engels spreekt men van :
Analoog:
Bij de radiale standaardafwijking (RSA of in het Engels RSD) wordt er een combinatie gemaakt van de horizontale standaardafwijking (sx) en de verticale standaardafwijking (sy). In feite gaat het hier om de vierkantswortel uit de som van de kwadraten.
![]()
De radiale standaardafwijking
wordt beschouwd als de meest efficiënte manier om de grootte
van een groepering te beoordelen omdat de invloed van enkele "flyers"
op het totale resultaat beperkt wordt. Het geeft een goede basis om
verschillende groeperingen te vergelijken. Ook geeft het een idee van
de mogelijkheid van een wapen om te groeperen ( dus van de precisie van
een wapen).
In de meeste gevallen is de groepering cirkelvormig. Dat wil zeggen dat
de horizontale en verticale standaardafwijkingen aan elkaar gelijk zijn
(of toch dat de waarden zeer dicht bij elkaar liggen) dus sx=sy .
In dit geval kunnen we zeggen dat:
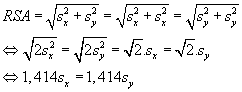
Dit is een systeem dat veel
gebruikt wordt bij de kwaliteitscontrole van munitie. De verwachte
cirkelvormige fout wordt gedefinieerd als de cirkel met als middelpunt
het GIP en diameter het CEP waarin 50% van de impacten. van een groot
aantal schoten (theoretisch oneindig veel) vallen.
Op welke manier kan men de CEP berekenen? De methode is omslachtig maar
eenvoudig. Daar het gaat om een cirkel met als middelpunt het GIP, moet
men eerst de coördinaten van het GIP berekenen. Vervolgens
gaat men de afstand van ieder schot tot het GIP berekenen en de
verkregen afstanden rangschikken volgens grootte. Men zoekt de mediaan
(het getal waarbij 50% van de berekende afstanden kleiner en 50% groter
is, en men heeft zo de grootte van de straal van de cirkel berekend.
Deze straal maal twee geeft de diameter van de CEP.
De gemiddelde straal wordt bekomen door het gemiddelde te nemen van alle individuele afstanden van de verschillende invalspunten tot het GIP. Om die te berekenen maken we de som van alle individuele afstanden tot het GIP en delen die door het aantal schoten:
![]()
Gewoonlijk gaat twee maal de gemiddelde straal groter zijn dan de CEP.
![]()
De maximale spreiding wordt gedefinieerd als de grootste afstand tussen twee impacten in de groepering. Deze maximale spreiding kan in alle richtingen gemeten worden. Let wel op dat dit niet noodzakelijk de diameter is van de kleinste cirkel die alle impacten omschrijft. De ES wordt gewoonlijk gemeten met een schuifpasser maar kan ook berekend worden en wel op de volgende manier:
We maken koppels van invalspunten en berekenen telkens de afstand tussen beiden. Indien men met een computer werkt dan kan men een programma maken dat deze berekeningen uitvoert voor alle mogelijke koppels, het volstaat dan het grootste resultaat te nemen. Indien de berekeningen niet automatisch gebeuren door een computer dan kan men zich beperken tot de koppels die in aanmerking komen om het grootste resultaat te geven.
![]()
De omschrijvende cirkel wordt
gedefinieerd als de kleinste cirkel die alle impacten in de groepering
omsluit. De omschrijvende cirkel zal niet altijd hetzelfde zijn als de
maximale spreiding alhoewel het verschil gewoonlijk zeer klein zal
zijn.
Hou er ook rekening mee dat het middelpunt van de omschrijvende cirkel
meestal niet het GIP is.
De diameter van de RCC is moeilijk te berekenen, we kunnen zeggen dat
we de afstand zoeken van twee schoten die ver uit elkaar liggen, er het
middelpunt van bepalen en dan nagaan of de afstand van ieder
individueel schot tot dat middelpunt kleiner of gelijk moet zijn aan de
helft van de afstand tussen het oorspronkelijk koppel. Als er aan deze
voorwaarde voldaan is heeft men de RCC gevonden.
Als de afstand van een enkel schot tot dat middelpunt echter groter is
dan de helft van de afstand tussen het oorspronkelijk koppel, dan zal
het middelpunt van de RCC gelegen zijn op de middelloodlijn van de
verbindingslijn van het oorspronkelijk koppel en wel zodanig dat de
afstand van de drie impacten tot dat middelpunt gelijk is.
Hierbij wordt gewoon de afstand tussen de twee horizontaal het verst uit elkaar liggende impacten opgeteld bij de afstand van de twee verticaal het verst uit elkaar liggende impacten. Het komt neer op de breedte en de hoogte van de rechthoek die alle schoten bevat en waarvan de zijden evenwijdig lopen met het coördinaten stelsel (ofwel horizontaal en vertikaal zijn).
Hierbij nemen we de diagonaal van de rechthoek die onder punt 8 besproken werd.
Ofwel:
![]()
Hier gaan we gebruik maken van de hoek waaronder we de ES van een
groepering zien op een bepaalde afstand, meer bepaald de afstand op
dewelke we de schoten gelost hebben. Deze manier van meten wordt,
weliswaar op een vereenvoudigde, benaderende manier veel gebruikt in de
Angelsaksische landen.
Een cirkel heeft 360graden (360°)en ieder graad wordt opgedeeld in 60 minuten (60').
Bij 1MOA wordt dus een stukje van de omtrek gezien met een lengte van de straal maal 2PI gedeeld door (360 maal 60).
Als we deze berekeningen uitvoeren met een straal van 100 m dan krijgen we voor 1MOA een ES van 2,908882 cm.
Als we de berekeningen uitvoeren met Imperiale maateenheden dan wordt
voor een straal van 100 yds (yards) 1MOA gelijk aan 1,047198 inch. Ik
zei in het begin van dit punt dat de benaderde waarde veel gebruikt
wordt in de Angelsaksische landen, ik bedoel hiermee dat men gewoonlijk
1MOA gelijk stelt aan 1 inch op 100 yards. Zoals we zien in de
berekeningen zit men er dan iets meer dan 4,7% naast).
Om de berekeningen uit te voeren bepaalt men eerst de maximale spreiding (ES) en de afstand waarop er geschoten werd. In het metrisch stelsel wordt het aantal MOA van de groep dan:
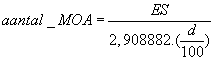
Waarbij de ES gemeten of berekend wordt in centimeter (cm) en d gelijk is aan de schootsafstand uitgedrukt in meter (m).
In Imperiale maateenheden wordt de formule:
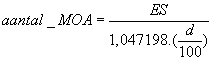
Waarbij de ES gemeten of berekend wordt in inches (inch of ") en d de schootsafstand is in yards (yds).
De vereenvoudigde, benaderende formule in Imperiale waarden wordt:
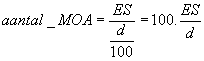
Waarbij de ES gemeten of berekend wordt in inches (inch of ") en d de schootsafstand is in yards(yds)
De MilDot wordt in militaire
middens gebruikt bij vizieren op scherpschuttersgeweren. Gewoonlijk
worden op de kruisdraad in de kijker merktekens aangebracht waarvan de
tussenafsta,nd overeenstemt met een vast bepaald aantal MilDot. Op deze
manier is de schutter in staat om met een eenvoudige berekening de
juist afstand te bepalen als hij de werkelijke grootte van het doel
kent en virtuele grootte in MilDot kan aflezen op zijn kruisdraad.
Naast deze eerste toepassing kan de MilDot ook gebruikt worden als grootte-aanduiding van groeperingen.
In tegenstelling met wat men zou denken is de Mil in MilDot geen
afkorting van militair maar van "milliradiaal" (een duizendste van een
radiaal, een hoekmaat waar bij 360° gelijk is aan 2PI radiaal).
Om dit te illustreren nemen we een cirkel met een straal van 1000m de
omtrek van een dergelijke cirkel is 1000 x 2PI meter. Als we nu gaan
berekenen welke grootte we zien met 1 MilDot gebruiken we volgende
formule:
![]()
De formule om de grootte (ES) van een groepering uit te drukken in MilDot wordt:
![]()
Waarbij de ES uitgedrukt wordt in millimeter (mm) en de afstand d in meter.
Om de afstand te schatten met een kijker met aangepaste kruisdraad, meet men het aantal MilDot waaronder men het doel ziet (bijvoorbeeld : 2 MilDot) we weten dat het doel 1m80 groot is (of 180 cm of 1800 mm) de afstand wordt dan: 1800/2= 900m
Een doel dat zich verplaatst met een snelheid van 3,6 km per uur evenwijdig met ons op 500 m afstand , we weten dat onze kogel er ongeveer 0,6 seconde zal over doen om daar te raken. In 0,6 seconden legt het doel 0,6 meter af, 0,6 meter op 500 meter is 1,2 meter op 1000 meter we moeten dus 1,2 MilDot voor het doel mikken om het te treffen op 500 meter.
Wanneer we groeperingen meten, kunnen we dat doen op twee manieren. We kunnen de buitenste merktekens van een groep nemen.
Bijvoorbeeld :
Als we echter de gegevens gaan
gebruiken voor berekeningen moeten we de afstand d weten tussen de
centers van de schoten d(ctc).